by

7.5 Area Between Curvesap Calculus



7.1 Area Between Two Curves(13).notebook. (183k) Jeffrey Cook.

  1. Home Calendar Q1 Q2 Q3 Q4 Review FRQ from AP Smacmath PC Calendar 7.5 Area Between Curves. 7.5 Area Between Curves.
  2. Calculus Name Date Period ©R D220 U1x3Q CKsu XtSah JSWoLfYtGwVaRrUe8 LMLRCQ.e n 6Atl 8lR or Si6gSh 8tDsm crQehsVeBrLv Pe9d H.d Area Between Curves Practice For each problem, find the area of the region enclosed by the curves. 1) y = − x y = 2 x x = 0 x = 4 x y −8 −6 −4 −2 2 4 6 8 −8 −6 −4.
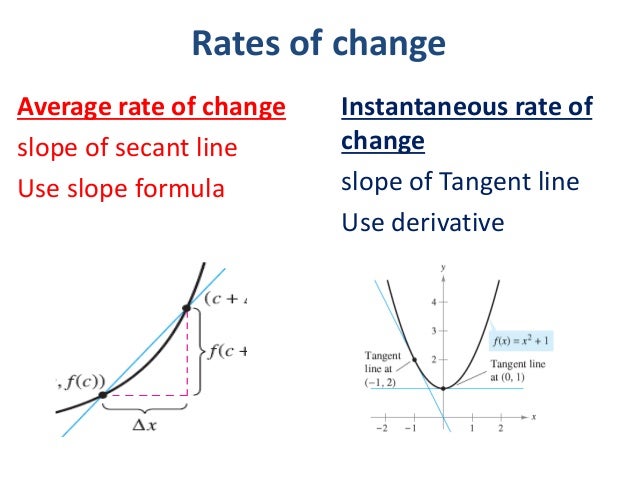
  3. 2.1.3 Determine the area of a region between two curves by integrating with respect to the dependent variable. In Introduction to Integration, we developed the concept of the definite integral to calculate the area below a curve on a given interval.
  4. AP Calculus: Area Between Two Curves Name: Sketch the graph of each equation, and then use your sketch to set up the integral to find the area between the curves. Use a calculator to evaluate your integral. ( )= 2+2, =−, =−2,and =1 2. ( )=6− 2and ( )= 3.
Show Mobile NoticeShow All Notes7.5 Area Between Curvesap CalculusHide All Notes
You appear to be on a device with a 'narrow' screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best views in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (should be able to scroll to see them) and some of the menu items will be cut off due to the narrow screen width.

7.5 Area Between Curves Ap Calculus Calculator

Section 6-2 : Area Between Curves

7.5 Area Between Curvesap Calculus
  1. Determine the area below (fleft( x right) = 3 + 2x - {x^2}) and above the x-axis. Solution
  2. Determine the area to the left of (gleft( y right) = 3 - {y^2}) and to the right of (x = - 1). Solution

For problems 3 – 11 determine the area of the region bounded by the given set of curves.

  1. (y = {x^2} + 2), (y = sin left( x right)), (x = - 1) and (x = 2) Solution
  2. (displaystyle y = frac{8}{x}), (y = 2x) and (x = 4) Solution
  3. (x = 3 + {y^2}), (x = 2 - {y^2}), (y = 1) and (y = - 2) Solution
  4. (x = {y^2} - y - 6) and (x = 2y + 4) Solution
  5. (y = xsqrt {{x^2} + 1} ), (y = {{bf{e}}^{ - ,frac{1}{2}x}}), (x = - 3) and the y-axis. Solution
  6. (y = 4x + 3), (y = 6 - x - 2{x^2}), (x = - 4) and (x = 2) Solution
  7. (displaystyle y = frac{1}{{x + 2}}), (y = {left( {x + 2} right)^2}), (displaystyle x = - frac{3}{2}), (x = 1) Solution
  8. (x = {y^2} + 1), (x = 5), (y = - 3) and (y = 3) Solution
  9. (x = {{bf{e}}^{1 + 2y}}), (x = {{bf{e}}^{1 - y}}), (y = - 2) and (y = 1) Solution

Area between Curves

The area between curves is given by the formulas below.

Area = (int_a^b {,left| {fleft( x right) - gleft( x right)} right|,dx} )

for a region bounded above by y = f(x) and below by y = g(x), and on the left and right by x = a and x = b.

for a region bounded on the left by x = f(y) and on the right by x = g(y), and above and below by y = c and y = d.

Example 1:1

Find the area between y = x and y = x2 from x = 0 to x = 1.

(eqalign{{rm{Area}} &= int_0^1 {left| {x - {x^2}} right|dx} &= int_0^1 {left( {x - {x^2}} right)dx} &= left. {left( {frac{1}{2}{x^2} - frac{1}{3}{x^3}} right)} right|_0^1 &= left( {frac{1}{2} - frac{1}{3}} right) - left( {0 - 0} right) &= frac{1}{6}})

1

Find the area between x = y + 3 and x = y2 from y = –1 to y = 1.

(eqalign{{rm{Area}} &= int_{ - 1}^1 {left| {y + 3 - {y^2}} right|dy} &= int_{ - 1}^1 {left( {y + 3 - {y^2}} right)dy} &= left. {left( {frac{1}{2}{y^2} + 3y - frac{1}{3}{x^3}} right)} right|_{ - 1}^1 &= left( {frac{1}{2} + 3 - frac{1}{3}} right) - left( {frac{1}{2} - 3 + frac{1}{3}} right) &= frac{{16}}{3}})

7.5 Area Between Curves Ap Calculus Formulas

See also

Curvesap

7.5 Area Between Curves Ap Calculus Algebra

Area under a curve, definite integral, absolute value rules